The Plate Theory

Classically defined, chromatography is a separation process that is achieved by distributing the substances to be separated between a moving phase and a stationary phase. The moving phase may be a gas or a liquid and the stationary phase may be liquid or a solid providing the two phases are immiscible. Those substances distributed preferentially in the moving phase pass through the chromatographic system faster than those that are distributed preferentially in the stationary phase. As a consequence, the substances are eluted from the column in the reverse order of the magnitude of their distribution coefficients with respect to the stationary phase (the larger the distribution coefficient the longer the substance will remain in the column).

As the extent to which two substances are separated will depend on their relative retention in the chromatographic system, an expression for the retention volume of a solute, in terms of the distribution coefficient of the solute between the phases, will show how retention can be controlled. In order to derive an expression for the retention volume it is necessary to obtain the equation for the elution curve of a solute; that is, an equation that will relate the concentration of the solute in the chromatographic column eluent to the volume of mobile phase that has passed through it. Such an equation will describe the curve called the chromatogram as depicted in figure 24.

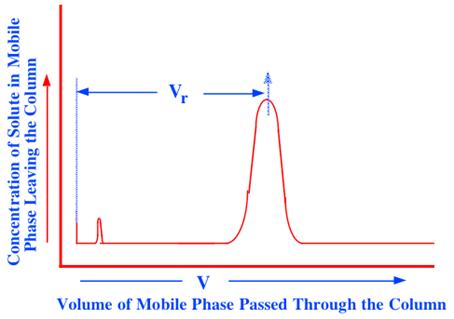
Figure 24. The Elution Curve of a Solute

If the elution-curve equation is developed, and the nature of f(v) identified, then by differentiating and equating to zero, the position of the peak maximum can be determined and an expression for (V_r) (the retention volume of the solute) can be obtained. The expression for (V_r) will disclose the factors that control the magnitude of solute retention and, thus, chromatographic separation. The plate theory, (9), provides the necessary equation for the elution curve of a solute. The original derivation of Martin and Synge, gives an exponential equation to describe solute retention that, unfortunately, is only approximate. However, Said (10), using the same basic concepts, but with a different mathematical argument, derived an explicit solution that was more accurate; it is the derivation of Said that will be given here. The plate theory applies to all chromatographic systems that utilize a column and will be pertinent to both gas and liquid chromatography.